Improvements for the Nonlinear Filtering Algorithms and their Application

The presence of noise in data is an inevitable consequence arising from factors such as incomplete data and the limited accuracy or resolution of sensors. These seemingly trivial noise elements significantly impede the comprehension and effective utilization of the underlying data. Fortunately, the field of noise filtering has made considerable strides in the development of robust algorithms to address this challenge.

This dissertation embarks on a comprehensive exploration of noise reduction techniques. Initially, it delves into fundamental mathematical principles before venturing into the realms of stability and optimization methodologies associated with both the Kalman Filter and Particle Filter.

In the latter segment of this research endeavor, attention is shifted towards Gaussian Processes (GP) and the adoption of the prevailing Hamiltonian Monte Carlo (HMC) method for hyperparameter inference. Recognizing the potential for substantial enhancement in algorithmic speed through the exploitation of data’s sequential nature, this study examines hyperparameter inference within the context of GP as a sequential process, wherein data arrives incrementally in an online fashion.

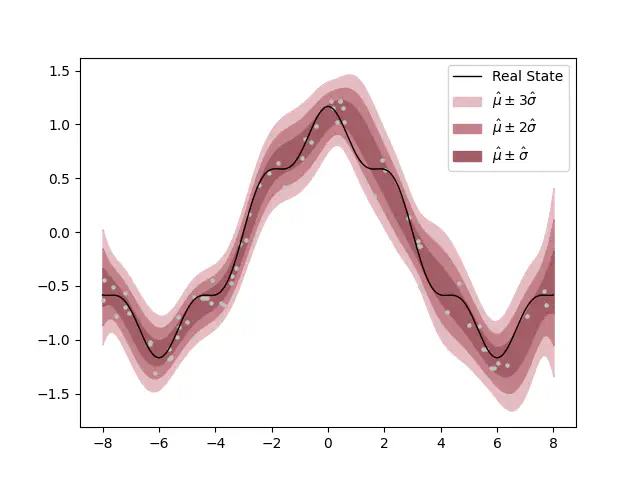
Empirical findings reveal that Sequential Monte Carlo (SMC) exhibits a marked efficiency advantage over HMC. Furthermore, the scope for further efficiency gains through the utilization of asynchronous computing remains unexplored. The incorporation of SMC into the GP framework necessitates addressing the challenge of sample impoverishment. This can be mitigated by introducing jitter into the hyperparameter samples, albeit at the cost of recalculating the covariance matrix and its inverse. Nevertheless, the overall computational efficiency of SMC significantly outpaces that of HMC, making it a compelling choice for practical applications.